The centuries-old dispute between the Geocentric Model and the Heliocentric Model Of the Solar System was finally put to rest by the German astronomer Johannes Kepler. In fact, he solved the riddle that we are living in the Heliocentric Model of the Solar System.
This means that the sun is at the center of our solar system, not The Earth. Well, Copernicus’s Heliocentrism also played a crucial role.
But, the role of Kepler’s law overshadowed that of Nicolaus Copernicus. Johannes Kepler’s Heliocentric Model showed that the orbits of planets are ellipses rather than circular.
Johannes Kepler Model of the Universe – The Heliocentric Theory
Here is the list of things I will be discussing in this article related to the keplerian model of the solar system.
- Historical View and Development of Kepler’s Law of Motion
- Comparison b/w Kepler Universe Model to Copernican Model
- Kepler’s Three Laws of Planetary Motion
- Eccentricity of the Planets
Historical View & Development of Kepler Solar System Model
Well, before the emergence of the Scientific Revolution or Copernican Revolution, the Aristotelian-Ptolemaic Universe was widely accepted as the working model of the Universe. Just for simplicity, let’s say it is the Aristotelian Universe.
According to the Aristotelian Universe or Earth-Centered Universe, the (stationary) earth is the center of the universe; and each planet within our solar system including the sun revolves around the earth.
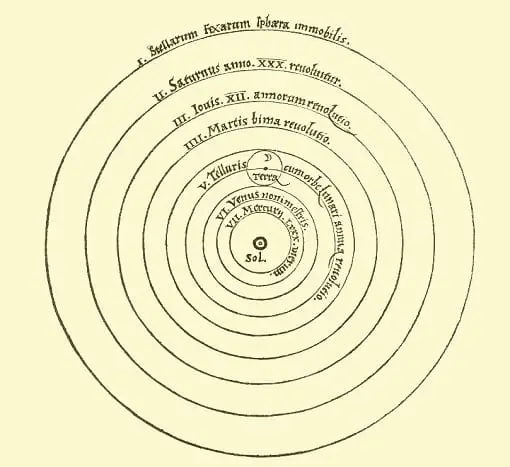
This geocentric model of the solar system was prevailing until the arrival of Copernican Heliocentrism.
Well, for those who don’t know, Nicolaus Copernicus was not the first person to proclaim that the sun is the center of the solar system, not earth. Therefore, every planet including earth revolves around the sun.
Related, Top 6 Obsolete cosmological Theories Of The Universe
It was the Greek astronomer Aristarchus of Samos who proposed the heliocentric model. Though there are no written works of him left now.
The heliocentric model was not originally accepted when it was first proposed by Aristarchus in the second-century bc. Simply, Because of the prevailing Aristotelian Universe.
In fact, as a contemporary of Aristotle, he always criticized Aristotle’s beliefs about the Earth-Centered Universe.
Problems in the Copernican Model
There were some notable problems in Nicolaus Copernicus’s heliocentric model. In the Copernican model, all the planets revolve around the sun in a circular motion which was enhanced by Johannes Kepler.
Of course, with the help of his mentor Tycho Brahe’s orbital calculation. In order to know more about Tycho Brahe’s works, You can check this article.
Later, Sir Issac Newton showed that Johannes Kepler’s laws of planetary motion are the direct consequence of Newton’s Law Of Gravitation which governs the forces between two massive objects.
Editor’s Choice: 6 Newton’s First Law of Motion Examples in our Daily Life
Comparison b/w Kepler Universe Model to Copernican Model
Although, both Johannes Kepler Heliocentric model and Copernican model contradicted the classical view of the Aristotelian-Ptolemaic Universe. Yet, there were some ideological differences between them; such as:
- In the Copernican Model, all planet revolves around the sun in a circular orbit. While on the other hand; in Kepler Universe Model, all planet revolves around The Sun but in a flattened circular orbit which means an elliptical orbit.
- Copernican Model states that the sun is located at the center of orbit. Whereas, Johannes Kepler’s Heliocentric model states that the sun is located at one of the foci of an elliptical orbit.
- In the Copernican Model, the speed of the planet in orbit remains constant. While on the other hand; in Johannes Kepler’s Heliocentric Model, the speed of the planet in orbit is not constant but the area speed remains constant.
Kepler’s Three Laws of Planetary Motion
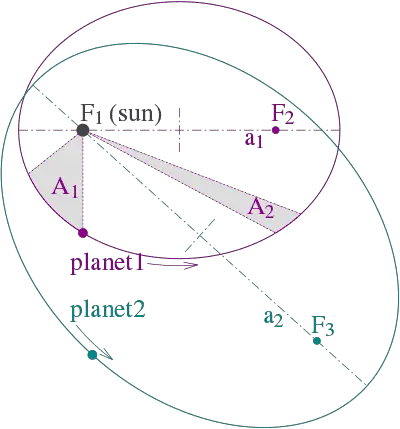
Johannes Kepler’s proposed solar system model has three 3 important laws. In fact, the importance of the sun in Kepler’s laws of motion can be seen in these three laws. Kepler’s Three Laws Of Planetary Motion can be described as follow:
Kepler’s First Law of Planetary Motion
When planets travel in an elliptical orbit around the sun with the sun located at one of the foci is known as Kepler’s First Law Of Planetary Motion. That’s why Kepler’s first law is also known as the law of ellipses.
Mathematically, according to Kepler’s first law, an ellipse can be represented by:
where,
r = distance from the sun to the planet

ε = eccentricity of an ellipse
θ = angle of the planet’s current position from its closest approach, as seen from the sun.
Kepler’s Second Law of Planetary Motion
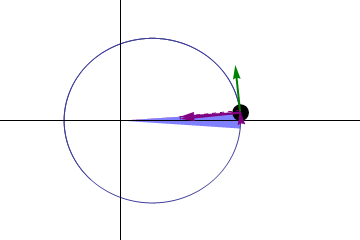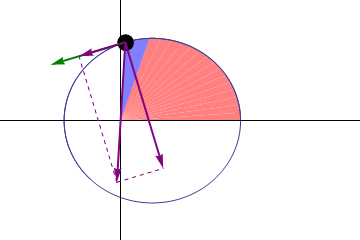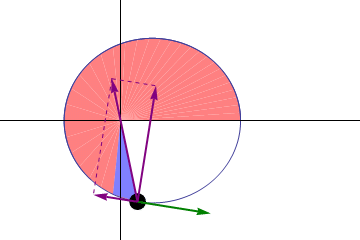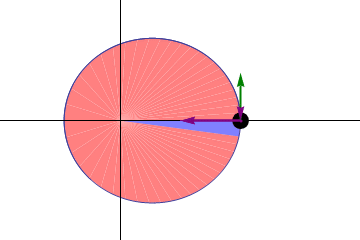
In planetary motion, the line joining the planet and the Sun sweep out equal areas in equal intervals of time. This is a direct consequence of Kepler’s second law of planetary motion. That’s why Kepler’s second law of planetary motion is also known as the law of equal areas.
Kepler’s Third Law of Planetary Motion
According to Kepler’s third law, the square of the time period of a planet is proportional to the cube of the semi-major axis of its orbit. That’s why Kepler’s third law of planetary motion is also known as the law of harmonies.
Well, mathematically, Kepler’s third law can be represented by the formula:
where,
M = mass of the sun
m = mass of the earth
G = gravitational constant
P = time taken by a planet to complete an orbit around the sun
a = mean value between the maximum and minimum distances between the planet and the sun.
Eccentricity of the Planets
The Eccentricity of the Planet is the ratio between the distance from the center to the focus divided by the semi-major axis. ε is the symbol of Eccencrity.
Well, it can be divided into two groups. Perihelion i.e. the closest point of a planet to the sun. On the other hand, Aphelion i.e. the farthest point of a planet to the sun.
Conditions for Eccentricity
- If ε = 0, then the planet’s orbit will be circular; the same as Copernican Heliocentrism
- Or, 0 < ε > 1, then the planet’s orbit will be elliptical
- If ε = 1, then the orbit will be parabolic
- Or, if ε > 1, then the orbit will be hyperbolic
That’s it for this post. If you like this article, share it if you like, like it if you share it. You can also find us on Mix, Twitter, Pinterest, and Facebook. Hey man, If you have come this far, do give us feedback in the comment section. It would make my day. Cheers!!!
You might also like:
- Geocentrism vs Heliocentrism in Tabular Form
- Difference Between Uniform and Non-uniform Motion with Examples
- Practical Curvilinear Motion Examples: Insights and Applications


Elliptical orbits are total rubbish.
‘G’ has never been proved as it removes effect of mass from equation’ [ K/10^-10]
There is no “PROOF” that gravity exists between SPACE masses.
Equation derivations are based on pure circular motion e.g. one ‘r’.
Central mass of orbits moved to the eccentric point where there is “NO MASS”